Self-Attention
要解决的问题:之前的网络结构支持的输入都是一个Vector,如果Input是个vector set,而且不同的vector set大小不一样,那么网络可能无法处理
- Input:N个vector
- Output有以下几种:
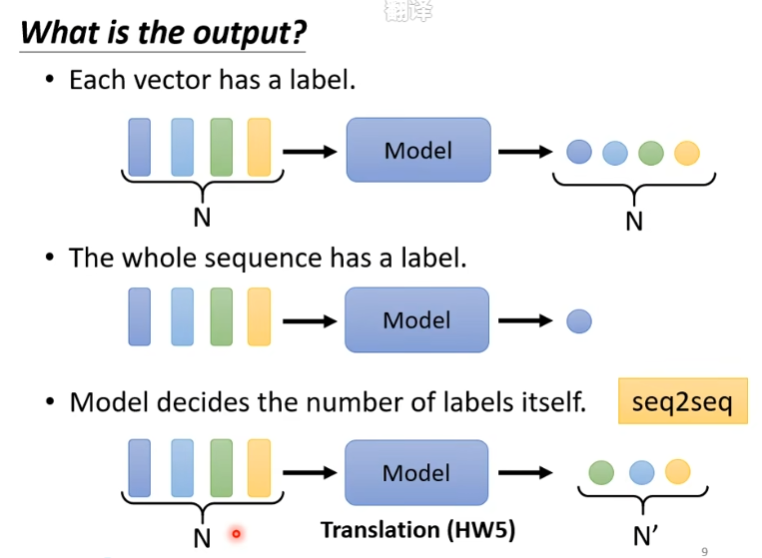
- N个class label(sequence labeling)
- 1个class label
- N’个label,模型自己学习他要输出多少个,又称为seq2seq Sequence Labeling
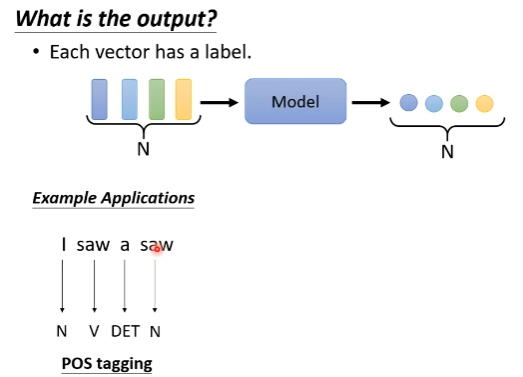
例子一: POS 词性标注
要输入一个句子,句子中的每一个词用embedding vetor表示
输出与输入维度一样大,是每一个input vector的分类
以上述Sequnce Labeling任务举例,如果用简单的fully connected network来做,那么FC network看到上文中的两个saw,同样的input vactor,自然给出的output label是一样的,不会考虑上下文信息。
当然,可以对FC稍加改造,让它通过一个window能够考虑邻居的信息,但是没有办法让FC看到全文信息后再输出(window非常非常非常大也不是不行,但是没必要,计算资源和速度会有限制)
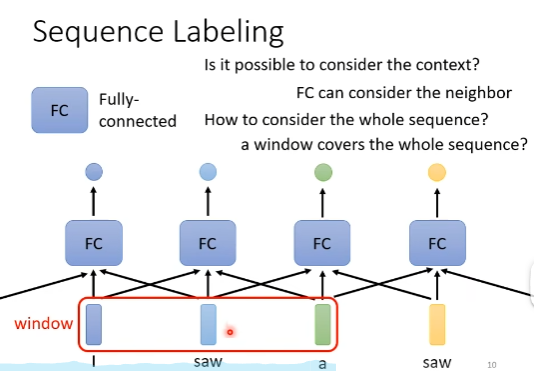
为了解决这样的问题,同时保证训练效率,可以通过Self-Attention机制来实现,让模型能够考虑全文的context
基本网络结构:
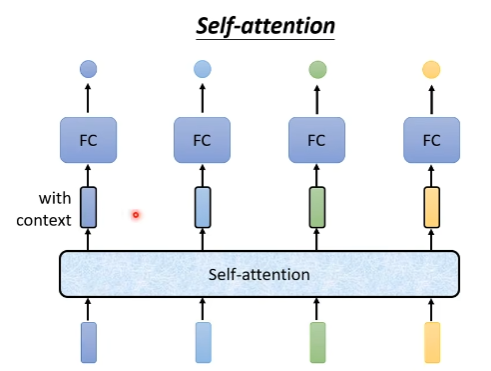
input:vector sequence(可以是真的input data,也可以是已经经过处理的hidden layer的output vactor)
中间 output(中间黑框的vector):表示基于输入,充分考虑全文context后的输出vector
- Self-attention layer用于考虑全文context的信息,FC layer主要用于考虑对应位置的局部信息。
Attention计算步骤及思路
- 首先确定self-attention layer的input、output
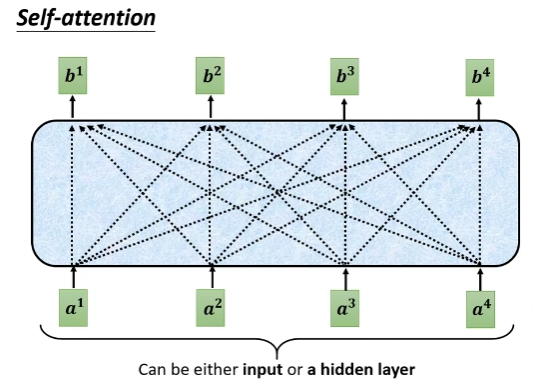
给定一个vector sequence A(a1, a2, a3, a4),输出另一个vactor sequence B(b1, b2, b3, b4),且每一个b_i都是考虑了所有A得出的向量
以计算b_1说明attention的计算过程,其他的b_j计算方法同理
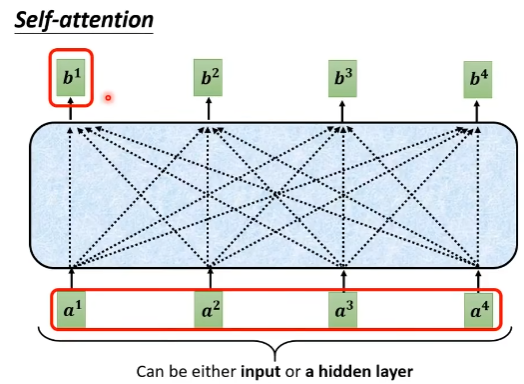
- 计算其他vector与a_1的相关性(就是attention score)
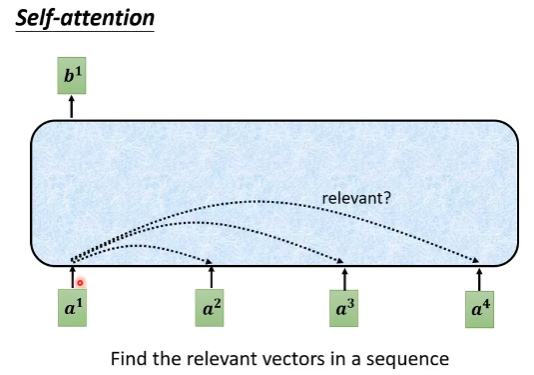
根据a_1,找到整个sequence中有相关性的部分。通过这种机制可以不用一个大window,也能考虑到所有sequnce context包含的信息
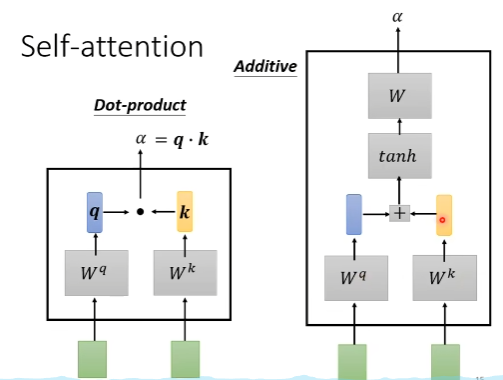
计算2个vector的相关性alpha
- 方法1:a_i,a_j与W^q, W^k相乘后transform得到的q, k向量做点乘
- 方法2:a_i,a_j与W^q, W^k相乘后得到的q, k向量做拼接后激活,并通过W做transform
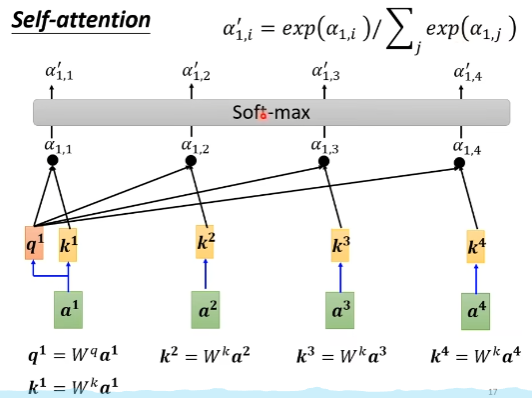
利用上述计算方法,计算a_1与每一个a_j的attention score alpha
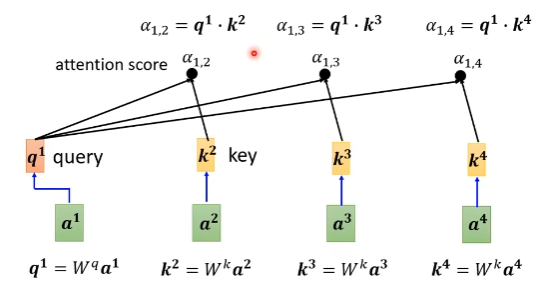
如何理解query和key?
答:现在我们要计算a_1与其他a_j的相关性,可以联想到搜索引擎中的query,任务就是找到与query最像的key
- 然后对每一个alpha进行softmax归一化,得到alpha’,这里也可以使用其他的归一化方法
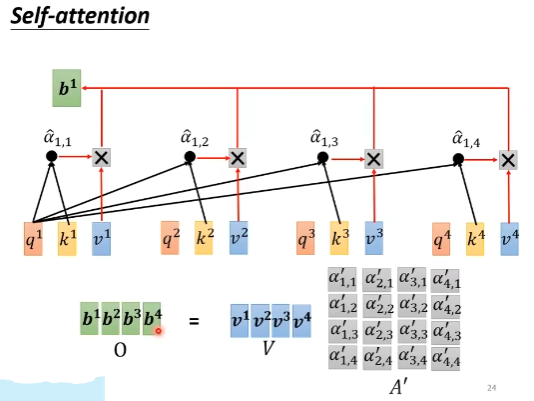
- 根据alpha‘ 抽取attention中的信息,计算b_1, Attention的影响会在最终的输出b_1中体现
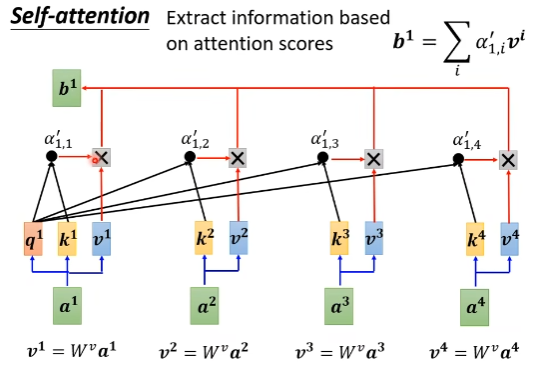
如果a_1和a_2的相关性很强(attention alpha’_1,2很大),那么最终b_1的值基本上是由v_2的值决定
从矩阵运算的角度来看Attention的计算过程
对比RNN,self-attention机制的一大优化点在于可以并行化。通过矩阵运算的视角看Attention的计算来理解如何并行
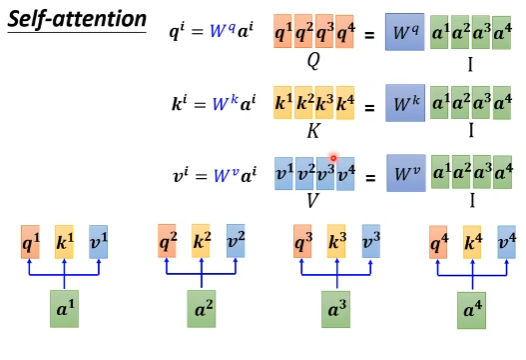
通过a,得到q、k、v
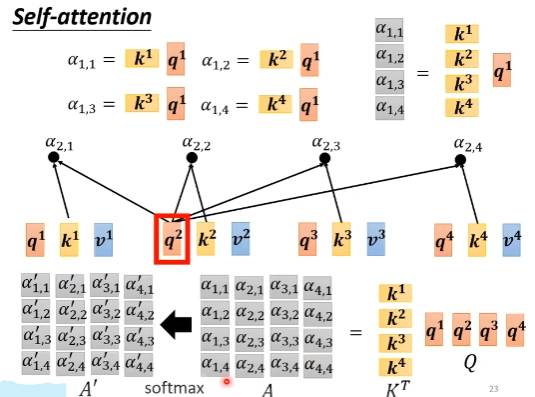
计算alpha和alpha’
计算b
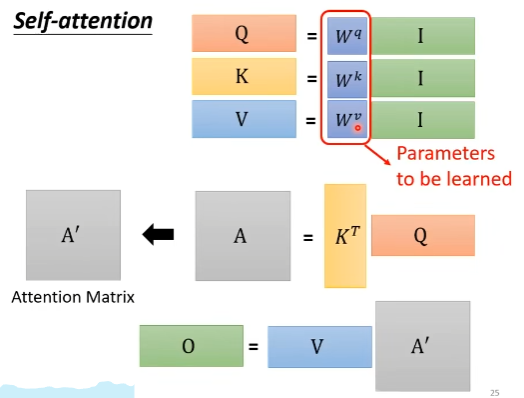
将上述过程在抽象一下,过程如下所示,基于输入Matrix I,经过矩阵运算后得到输出Matrix O,所需要学习的参数只有W^q, W^k,W^v
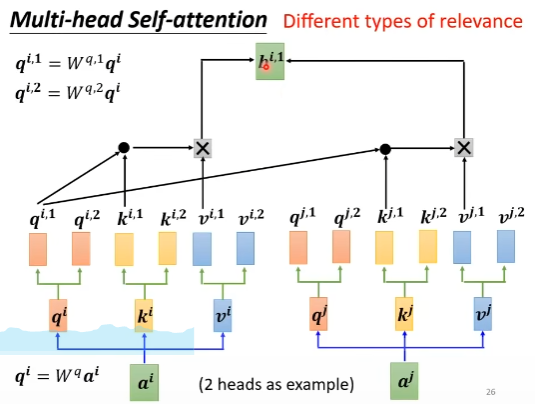
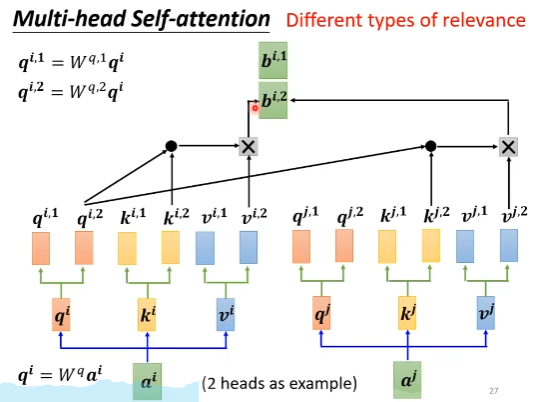
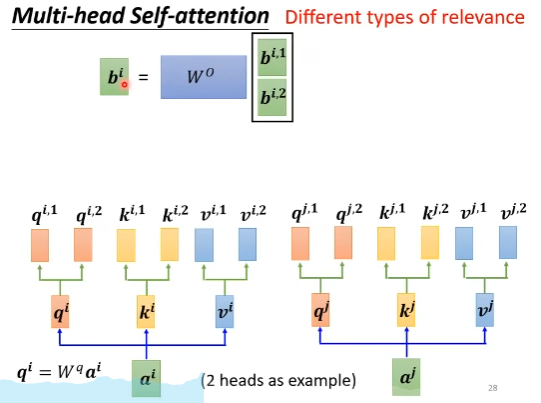
延伸:Multi-head self-attention
idea:attention就是在用query在找vector之间的相关性,有时候相关性有多种类型,因此可以用不同的query来获得vector之间的不同相关性